Mark Newbold's Rhombic Dodecahedron Page
This page discusses the Rhombic Dodecahedron and its relationship to the 4-dimensional hypercube.
3D glasses (red-blue) are required to view this page properly.
The red filter should be on the left.
The images with a green background are 3D images. So is the page background.
I am also experimenting with a Stellated Dodogahedron. Please check it out.
 This is a screen-shot of the hypercube applet.
The orientation of the hypercube has been adjusted (in 4-space) so that
the 3-space image forms a perfect "rhombic dodecahedron" (plus some
extra internal lines emanating from the center).
This is a screen-shot of the hypercube applet.
The orientation of the hypercube has been adjusted (in 4-space) so that
the 3-space image forms a perfect "rhombic dodecahedron" (plus some
extra internal lines emanating from the center).
A "dodecahedron" is a polyhedron with 12 faces (do=2, deca=10, hedron=base).
Most people associate the word "dodecahedron" with the pentagonal dodecahedron.
Various other dodecahedra are known.
The faces of the rhombic dodecahedron
are all identical rhombuses (a rhombus is a parallelogram with all edges equal,
i.e. a squashed square). It is not considered a "regular" polyhedron because the vertices are
not all the same. Some of the vertices join 3 faces and some join 4 faces.
How to Make your own Rhombic Dodecahedron
You can make one of these for your very own by playing around with the hypercube applet.
Once you have made it, you can admire it from all angles.
If you have read the user interface instructions for
the hypercube applet, you know that you can rotate the object in 3-space by dragging with the
mouse. You can rotate it in the 4th dimension by holding down the shift key and dragging
with the mouse. By alternating between these two types of rotations, you can get the
hypercube oriented as shown.
Your goal is to get two points to exactly coincide in the center (when viewed from all 3-space angles).
The points that you want to coincide are opposite corners of the hypercube (the shortest path of edges
from one to the other is 4 edges long).
A 3-Dimensional Analogy
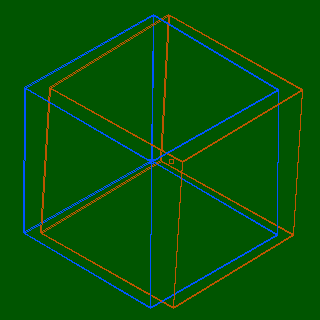 This screen shot is also taken from the hypercube applet. In this case,
I adjusted the hypercube orientation so that its projection is
a simple cube in 3-space.
This screen shot is also taken from the hypercube applet. In this case,
I adjusted the hypercube orientation so that its projection is
a simple cube in 3-space.
You can do this too but you won't get exactly the same result.
I cheated a little by modifying some hard-coded parameters in the applet
(I multiplied the eye-to-screen distance and eye-to-nose distance
by 100 so as to make the 3-space projection almost orthogonal.)
If you view this image with your 3D glasses, you see a 3-dimensional cube.
(The 4-dimensional aspect is concealed and is irrelevant to this part of the discussion.)
Now close your left eye so you see only the blue image. Note that it is
a perfect hexagon (plus some extra internal lines emanating from the center).
By closing one eye, you have projected the 3-dimensional cube onto the 2-dimensional
screen.
In summary, the analogy is:
- A rhombic dodecahedron is a projection of a 4-cube onto 3-space.
- A hexagon is a projection of the 3-cube onto 2-space.
You can do the same thing with all the higher-dimensional hypercubes.
Projecting them onto 3 dimensions produces various increasingly complicated
polyhedra, all having paralelograms for faces.
Recipe for a Rhombic Dodecahedron
A solid rhombic dodecahedron doesn't photograph well. It is hard to visualize
its shape from the faces which are visible. The following images are intended
to give an intuitive understanding of the thing.
Recipe Ingredients:
2 identical cubes, greenish on the outside, purplish on the inside (preferably fresh, with no mushy spots)
 Using a very sharp knife, slice one of the cubes into 6 identical pyramids as shown.
Using a very sharp knife, slice one of the cubes into 6 identical pyramids as shown.
 Line up the 6 pyramids with the 6 faces of the remaining cube.
(You need 7 hands to do this.)
Line up the 6 pyramids with the 6 faces of the remaining cube.
(You need 7 hands to do this.)
 Smush the pyramids onto the cube so they stick. Smooth out the junctions
so they are invisible. Chill before serving.
Smush the pyramids onto the cube so they stick. Smooth out the junctions
so they are invisible. Chill before serving.
As I said, the rhombic dodecahedron doesn't photograph well.
It is helpful to compare the features of this image with those of the previous image.
You might think that this procedure would produce an object with 24 faces
since each of the 6 pyramids has 4 exposed triangles. But in fact, pairs
of triangles are co-planar so they join to form 12 rhombuses.
A Question
On this page, I asked if anyone could provide a simple explanation of why the
rhombic dodecahedron is a projection of the hypercube. Here are the responses
I have received:
- Russell Towle has provided a discussion of this issue.
- David Christie has pointed out that
H.S.M. Coxeter discusses this in section 13.8 of his book "Regular Polytopes"
(Coxeter01).
I haven't yet had a chance to try to understand it, or see whether his
explanation can be translated into non-mathematical terms.
Filling Space
Rhombic dodecahedra can be fitted together to fill space with no overlaps
and no gaps (a spatial tesselation or "honeycomb"). This is illustrated by
the background of this page, which shows some layers of a such a honeycomb.
For other honeycomb backgrounds, see Mark's Page
and my Java Page.
The following blank space is provided to allow unobstructed viewing of the background:



A spatial filling by rhombic dodecahedra occurs naturally in
garnet crystals.
I know of two explanations of why rhombic dodecahedra can fill space:
- Hypercubes can fill 4-space, just as cubes can be stacked to fill 3-space.
Since you can project a hypercube onto 3-space as a rhombic dodecahedron, you should
be able to project a 4-space tesselation of hypercubes onto 3-space to produce
a 3-space tesselation of rhombic dodecahedra.
- You can fill 3-space with alternate black and red cubes such that every black cube shares
its faces only with red cubes and vice versa (making a 3-dimensional checkerboard).
Slice up each of the red cubes into pyramids as in the recipe (above) and glue
the bases of these pyramids onto the adjoining black-cube faces. It is apparent that
this yields a 3-space tesselation by rhombic dodecahedra.
My Paper Model
I made a paper model of the rhombic dodecahedron, which helped me
to visualize the images on this page. I wouldn't use the recipe
I described above for making an actual model. To make a paper model, you need
to start with 12 identical paper rhombuses. The internal angles of the rhombuses
are 70.53 degrees and 109.47 degrees. (70.53 degrees is ArcCos(1/3)). For
more information about making paper models of polyhedra, see George Hart's
Paper Polyhedra Page.
VRML Models
If you have a VRML viewer, check out the VRML Rhombic Dodecahedron
listed on George Hart's Zonohedra Page.
George also has a VRML Compound of 5 Rhombic Dodecahedra listed on his
"Uniform Compounds of Uniform Polyhedra" page under the heading of
"Relatives of the 5 Cubes".
Compound of 5 Rhombic Dodecahedra
I have a Stereoscopic 3D view of the compound of 5 Rhombic Dodecahedra.
September 19, 1996
Eric Swab says:
"There is another (closely related) recipe for creating a Rhombic
Dodecahedron. Begin with a single cube, slice off an edge with a plane that
is parallel with that edge and passes through the mid-line of the 2 adjacent
faces. Then do the same with all the remaining edges and the form you are
left with is a Rhombic Dodecahedron."
January 28, 1997
Eric Swab says:
"I was looking at Critchlow's "Order in Space" p. 55, this morning and
discovered another recipe for the Rhombic Dodecahedron. Start with an
octahedron, lay on each triangular face an irregular tetrahedron which is
1/4 of a regular tetrahedron. These irregular tetrahedron are formed by
joining each vertex of the regular tetrahedron with its center. 4 irregular
tets are formed in this way and 8 are required to cover all 8 faces of the
octahedron."
February 10, 1997
Russell Towle says:
"In Mathematica, you can apply the Stellate command to the built-in
polyhedra. Using this command, and carefully choosing the parameter of
stellation, you can create Kepler's rhombic dodecahedron by stellating
either the cube or the octahedron. In each case it is as though we had
"balanced planes" across the edges of these solids, letting them cut one
another off. The analogous balancing, applied to a tetrahedron, gives a
cube, and applied to the icosahedron and pentagonal dodecahedron, gives
Kepler's rhombic triacontahedron, which is an isometric shadow of a 6-cube."
Russell has also pointed out that the Rhombic Dodecahedron under discussion here
should be referred to as "Kepler's Rhombic Dodecahedron" since there
are other Rhombic Dodecahedra. --MN
March 4, 1997
Matthew R. Kennedy says:
"You may wish to see ours [web site] (under construction) at
http://www.erols.com/mrkenn/index.html [this link no longer works]
in which we emphasize the unity between the parallel and perspective
projections of the hypercube in our "Inverted Projected Tesseract
Resonating Chamber" loudspeaker design (patented)."
March 10, 1997
George Olshevsky says:
"The RD also contains a 3-D projection
of the regular icositetrachorema (or 24-cell), the regular 4D polytope (or
polychorema) that consists of 24 octahedra. Twelve of the octahedra project
flat into the 12 face-planes of the RD (the short diagonal of each face
represents the square equator of the octahedron projected edgewise, so you
need these lines to be drawn in addition to the edges of the RD), and the
other twelve project into the somewhat flattened octahedra formed by a
trivalent vertex, the four vertices edgewise adjacent to it, and the center
of the RD. There are 6 such configurations within the RD, each representing a
pair of coincident octahedra--one from in front, the other from behind."
I had already noticed that my 24-cell Java applet seems to produce
a rhombic-dodecahedron. In fact, that is the start-up state of the animation.
If you click the "Stop" button very quickly after the applet starts, you
will see a rhombic dodecahedron. --MN
March 16, 1997
Stefan Scheller says:
"How to make a Rhombic Dodecahedron?
Simply intersect 3 cylinders orthogonally and
take the common solid which belongs to all 3 cylinders.
Well, it's a bit blown up..."
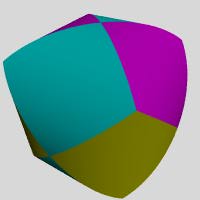 I tried it.
I tried it.
This is what I came up with (using a different color for each cylinder). --MN
September 6, 1997
Kevin Brown says:
"Another interesting fact about this shape is that it is the
"shape of coincidence" for four events. There is an article
on my web site about this."
September 28, 1997
Referring to George Olshevsky's note (above),
Eric Swab says:
"I was reminded that the cuboctahedron, the dual of the RD is also a "shadow" of the
24-cell.
November 9, 1997
Dr. Donald Carlson says:
"An infinite lattice of spheres can be modeled as a single sphere
inscribed in a unit cell with reflecting boundaries (i.e., a polyhedral
box of mirrors)." He notes that the Rhombic Dodecahedron is the
unit cell for the "face-centered-cubic" (fcc) close-packing of spheres.
For the full contents of Dr. Carlson's email, click here.
December 26, 1998
Mark Newbold (me) says: "I note that the 1977 Sci-Fi movie
Demon Seed
features a large Rhombic Dodecahedron which unfolds into octahedra and attacks a nerd.
The RD appears about 1 hour into the movie."
July 20, 2000
Ray Tomes says:
"In your page ... you discuss why
Rhombic Dodecahedra are space filling. My favorite way of thinking
about how they do this is to start with the famous Kepler sphere packing
problem, preferably by imagining oranges as usually stacked. Then apply
pressure so that the oranges are squashed until all the air is squeezed
out of the spaces between but the juice doesn't quite come out of the
oranges. The resulting shape is the space packing of Rhombic
Dodecahedra. Again, chill slightly before serving :)"
May 9, 2001
Ken Wauchope says:
"As a garnet crystal enthusiast I enjoyed visiting your rhombic
dodecahedron webpage. If you have a VRML2.0 browser you might be
interested in a presentation on garnet geometry I put together
recently for my rock and mineral club (also featuring the RD's
close cousin the Trapezoidal Icositetrahedron) including animations
of several of the geometric transformations your page discusses:
http://home.comcast.net/~kwauchope/garnet/index.html.
June 9, 2013
Piet Ruhe made a jitterbug out of RD's:
http://www.youtube.com/watch?v=T1vaO1tHNFY.
The ray-traced images on this page were made using POV-Ray.
The page background was produced with a Java applet.
Most of the information about polyhedra comes from H.S.M. Coxeter's book
"Regular Polytopes" (Coxeter01).
<Dogfeathers Home Page>
<Mark's Home Page>
Email:
Mark Newbold
This page URL:
http://dogfeathers.com/mark/rhdodec.html
This screen shot is also taken from the hypercube applet. In this case,
I adjusted the hypercube orientation so that its projection is
a simple cube in 3-space.
Using a very sharp knife, slice one of the cubes into 6 identical pyramids as shown.
Line up the 6 pyramids with the 6 faces of the remaining cube.
(You need 7 hands to do this.)
Smush the pyramids onto the cube so they stick. Smooth out the junctions
so they are invisible. Chill before serving.
I tried it.