I first noticed it in my HyperStar Java applet (applet settings are here). It turns out that there's something non-traditional about the version produced by the applet. That's what this web page is about.

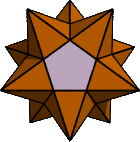
The Great Triambic Icosidodecahedron:

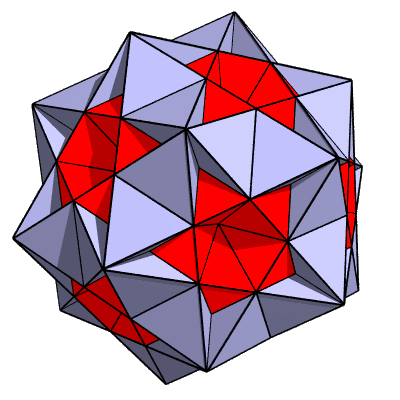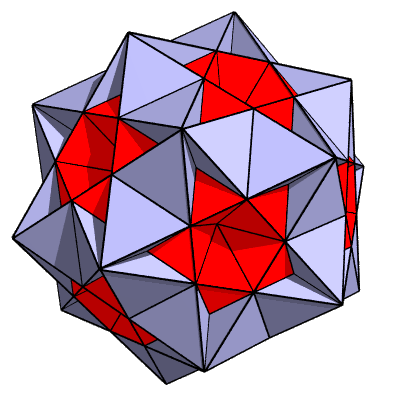
Wiggle Stereoscopy is used here to make the image look 3−dimensional.

It's a GIF animation that jiggles the polyhedron back and forth by 1 degree of rotation. If you want to stop the jiggling, try your browser's stop button.

I used POV−Ray, a freeware ray-tracer, followed by some fiddling in Photoshop.

In the most obvious topology, there are 20 regular triangles and 12 regular pentagons, with each edge joining a triangle to a pentagon. The vertices where 3 triangles and 3 pentagons meet are interesting places. If you make a small circuit around a vertex point, staying on the surfaces, you have to go around the vertex twice before you come back to your starting point. The vertex is a "branch point".

Fooling around with the HyperStar applet (morphing it by moving the section slider to a larger setting) reveals that the applet is working with a different topology. As you will see, the pentagons are non-standard (actually not pentagons at all) and are connected up in a different way. Each apparent vertex is actually actually a coincidence of 3 vertices, which are not "branch points".

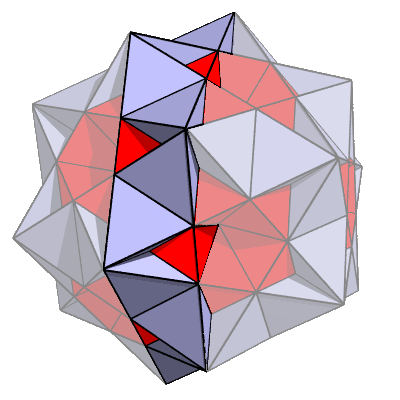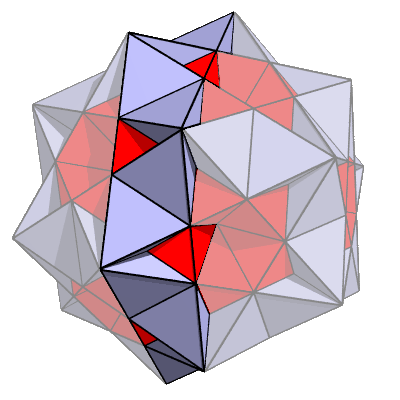To see how it works, we'll need to take a cross section of the polyhedron. The proposed cross section is emphasized here:

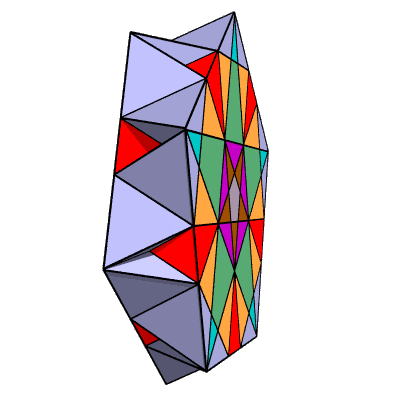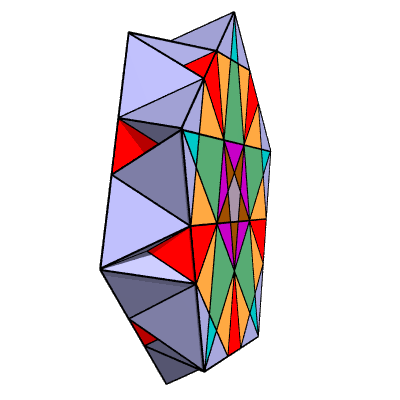Here's the cross section by itself:

The full polyhedron can be constructed out of six intersecting cross-sections, though many of the chunks are duplicated when you do this.

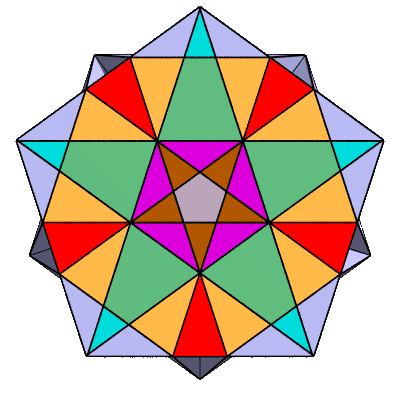Looking perpendicularly at it:

This incorporates chunks from shells 1 through 6 (referring to the applet's shell slider).

To get the shell number of a chunk, just add 1 to the number of lines you have to cross to reach that chunk from the center.

The pentagon in the center is actually a face of an embedded dodecahedron (shell 1):

It starts with shell 1 because the section setting is too large to pick up shell 0.

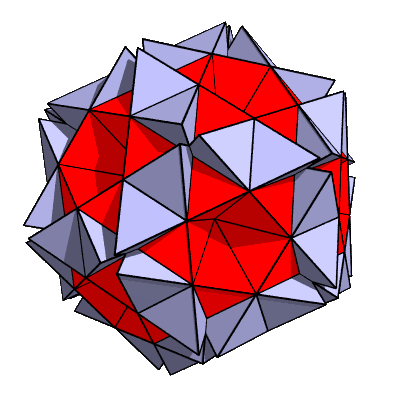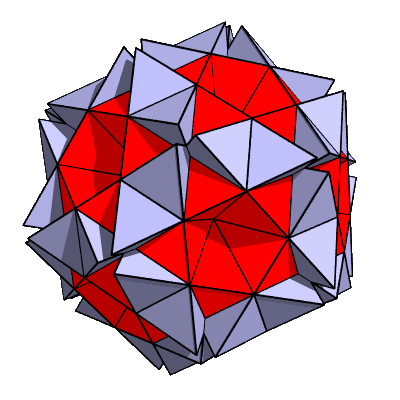
The brown triangles are faces of an embedded "small stellated dodecahedron" (shell 2), which has its front and rear points chopped off by the cross-sectioning process.

To make the non-standard topology apparent, we raise the applet's section slider to 0.880:

The triangles have separated so their vertices no longer touch.

Instead of a complicated vertex with a "branch point" that joins 3 triangles with 3 pentagons, we find that we have 3 simple vertexes, each joining a single triangle to 2 pentagons (but they aren't really pentagons anymore).

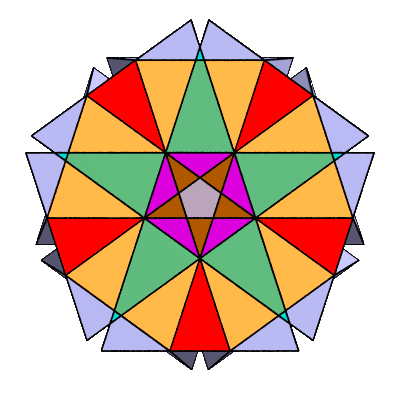Here's a cross-section of the 0.880 polyhedron.

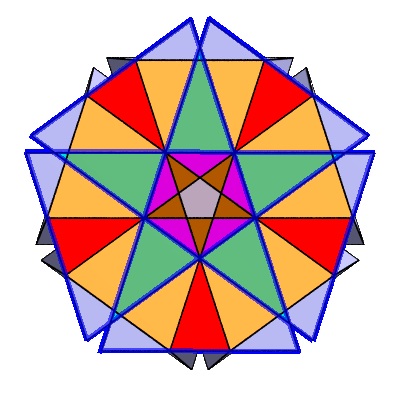What formerly appeared to be a pentagon turns out to be a 10-sided figure (a non-standard decagram). It's a lot like a standard decagram, except that the relative positions of the vertices are shifted. In the Great Triambic Icosidodecahedron, the vertices coincide in pairs, giving the appearance a pentagon with 5 vertices. In this diagram, they're shifted a little farther so they no longer coincide.

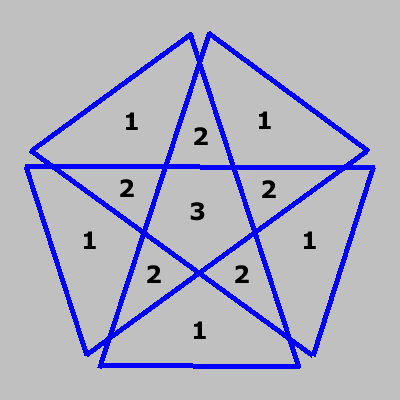Here's a line drawing. The numbers represent the "density". Since the surface crosses over itself, it's actually 3 layers thick at the center. If you make a circuit around the surface, you have to go around 3 times before you come back to your starting point.

This kind of thing isn't possible with real world materials, since they can't pass through each other. A benefit of model-making on the computer is that we are freed from such silly physical limitations.

The non-traditional "Great Triambic Icosidodecahedron" is a complicated object in the way its surfaces are connected together. The long internal edges of the decagram are connected to the internal edges of other decagrams of the polyhedron. The shorter external edges of the decagram are connected to triangles. If you stare at the diagrams for a while you can probably get a feeling for the way these shapes are connected together.

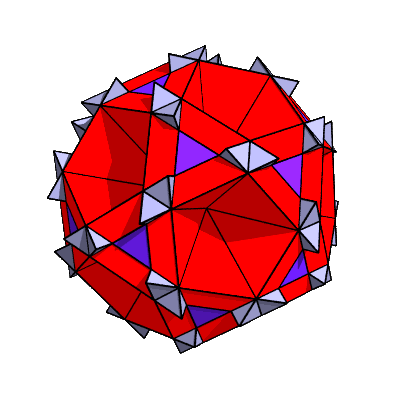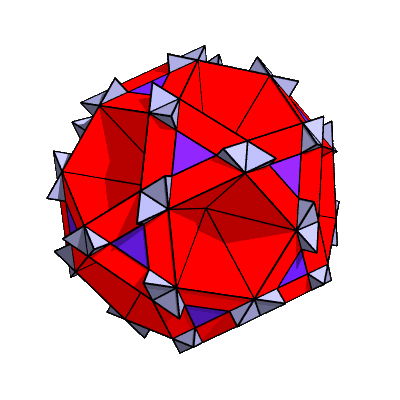Here's the polyhedron that results when the applet's section slider is raised to 0.910:

If you look at the same thing in the HyperStar Java applet, you will see pits form in the centers of the triangles. This is a consequence of the way the applet categorizes the chunks into shells. In this POV-Ray rendering, I borrowed some purple-colored tetrahedral chunks from shell 7 to fill in the pits.

To summarize: in this alternative topology the pentagons are replaced by non-standard decagrams (whose vertices coincide in pairs). The decagrams are joined to each other along their internal edges. The external decagram edges join to triangles.